Predicting with the Model Generator prediction (online) BLOCK
Predicting with the Model Generator prediction (online) BLOCK
There are several ways to provide input data for making predictions to the Model Generator prediction (online) BLOCK. The Model Generator How-To guides (Classification/Regression) explain a method that uses the Construct object BLOCK.
This page explains the methods listed below. Each example uses the scenario from the Making predictions section of the Model Generator How-To: Classification guide.
- Providing input data as files
- Providing input data from BigQuery
- Providing input data when externally executing Flows (application/json)
- Providing input data when externally executing Flows (x-www-form-urlencoded)
info_outline The various names used on this page (filenames, bucket names, dataset names, table names, etc.) can be freely configured. However, the input data's item names (including "key") should be set as shown.
Providing input data as files
This method uses input data prepared as YAML or JSON format text files.
In order to use the Model Generator prediction (online) BLOCK, this data will need to be set as a variable with data formatted according to certain specifications.
We will set our data to a variable using the Load to Variable from GCS BLOCK (GCP category). This BLOCK sets a variable as the contents of a file stored in Google Cloud Storage open_in_new (GCS). When the file's format is YAML or JSON, the variable's data will also be constructed according to that format. This process is shown in the image below.

The following example shows how to make predictions using input data prepared as a JSON format text file.
First, create a JSON format text file named iris_predict_data.json as shown below, then upload it to a GCS bucket (bucket name: magellan-sample).
{
"data": [
{
"key": "1",
"sepal_length": 5.9,
"sepal_width": 3.0,
"petal_length": 4.2,
"petal_width": 1.5
},
{
"key": "2",
"sepal_length": 6.9,
"sepal_width": 3.1,
"petal_length": 5.4,
"petal_width": 2.1
},
{
"key": "3",
"sepal_length": 5.1,
"sepal_width": 3.3,
"petal_length": 1.7,
"petal_width": 0.5
}
]
}
Create the following Flow on a Flow Designer:
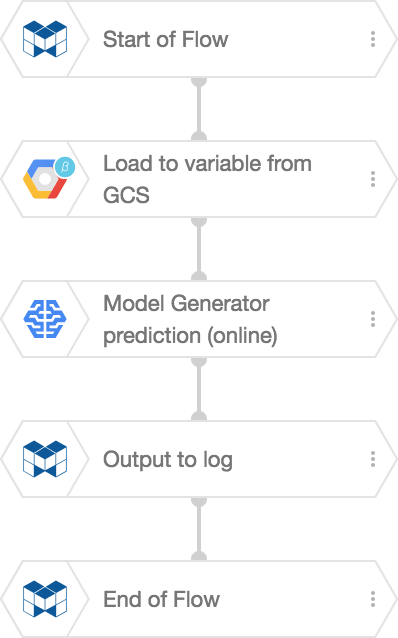
The Load to Variable from GCS BLOCK reads the contents of the text file. Then, the Model Generator prediction (online) BLOCK makes the predictions. In this example, we send the results to the logs section with an Output to log BLOCK.
Set the properties for each BLOCK as shown below. We’ve only included properties that need to be changed from default values in the chart.
| BLOCK | Property | Value |
|---|---|---|
| Load to Variable from GCS | Source file GCS URL | gs://magellan-sample/iris_predict_data.json |
| File format | JSON | |
| Results variable | _ |
|
| Model Generator prediction (online) | Model Generator | Select the Model Generator that will be used for the prediction |
| Input variable | _.content.data |
|
| Output variable |
info_outline We're using the same variable, |
|
| Output to log | Variable to output | _ |
Once you’ve created the Flow, save your Flow Designer and click the play_circle_outline button from the Start of Flow BLOCK's properties menu.
The following is a portion of the resulting log:
{
"predictions": [
{
"score": [
0.017455093562602997,
0.7145982980728149,
0.26794660091400146
],
"key": "1",
"label": 1
},
{
"score": [
0.0007236730307340622,
0.40548425912857056,
0.5937920212745667
],
"key": "2",
"label": 2
},
{
"score": [
0.9445222616195679,
0.05332513898611069,
0.0021526541095227003
],
"key": "3",
"label": 0
}
]
}
Providing input data from BigQuery
This method makes predictions using input data prepared as a BigQuery table.
As explained in the previous example, the Model Generator prediction (online) BLOCK requires input data that is stored into a variable. This data must be formatted according to certain specifications.
In this example, we’ll use an Execute query BLOCK to get data from BigQuery and set it as a variable formatted according to the Model Generator prediction (online) BLOCK's specifications.

First, prepare the following table in BigQuery:
| Item | Value |
|---|---|
| Dataset name | samples |
| Table name | iris_predict_data |
| Name | Type | Mode |
|---|---|---|
| key | STRING | NULLABLE |
| sepal_length | FLOAT | NULLABLE |
| sepal_width | FLOAT | NULLABLE |
| petal_length | FLOAT | NULLABLE |
| petal_width | FLOAT | NULLABLE |
| key | sepal_length | sepal_width | petal_length | petal_width |
|---|---|---|---|---|
| 1 | 5.9 | 3.0 | 4.2 | 1.5 |
| 2 | 6.9 | 3.1 | 5.4 | 2.1 |
| 3 | 5.1 | 3.3 | 1.7 | 0.5 |
Create the following Flow on a Flow Designer:
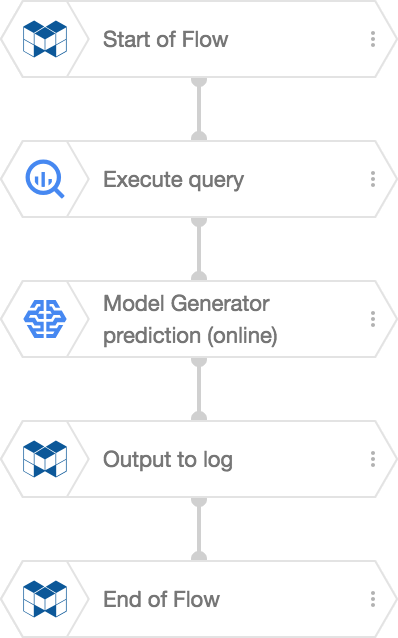
The Execute query BLOCK takes the input data from BigQuery and stores it into a variable. Next, the Model Generator prediction (online) BLOCK uses the data in this variable to make predictions. In this example, we send the results to the logs section using an Output to log BLOCK.
Set each BLOCK's properties as shown below. The chart only contains properties that need to be changed from their default value:
| BLOCK | Property | Value |
|---|---|---|
| Execute Query | SQL Syntax | Legacy SQL |
| Query |
SELECT key, sepal_length, sepal_width, petal_length, petal_width FROM samples.iris_predict_data |
|
| Results variable | _ |
|
| Model Generator prediction (online) | Model Generator | Select the Model Generator that will be used to make predictions. |
| Input variable | _ |
|
| Output variable |
info_outline We're using the same variable, |
|
| Output to log | Variable to output | _ |
Once the Flow is ready, save and execute the Flow by clicking the play_circle_outline button from the Start of Flow BLOCK's properties menu.
The following is a portion of the resulting log:
{
"predictions": [
{
"score": [
0.017455093562602997,
0.7145982980728149,
0.26794660091400146
],
"key": "1",
"label": 1
},
{
"score": [
0.0007236730307340622,
0.40548425912857056,
0.5937920212745667
],
"key": "2",
"label": 2
},
{
"score": [
0.9445222616195679,
0.05332513898611069,
0.0021526541095227003
],
"key": "3",
"label": 0
}
]
}
Providing input data when externally executing Flows (application/json)
This method uses input data sent when externally executing a Flow to make predictions.
External Flow execution refers to using a Web API to execute a Flow. The method for making predictions sets the Content-Type header to application/json in the HTTP request.
When externally executing a Flow, you can pass data as JSON text and set BLOCKS variables to various values from this data.
For example, you could set the variable var to the value 100 by using a request with its Content-Type header set to application/json and the body of the HTTP request set as the following JSON text:
{"var": 100}
The following JSON text would set the variable _ as prediction input data for Machine Learning:
{
"_": [
{
"key": "1",
"sepal_length": 5.9,
"sepal_width": 3.0,
"petal_length": 4.2,
"petal_width": 1.5
},
{
"key": "2",
"sepal_length": 6.9,
"sepal_width": 3.1,
"petal_length": 5.4,
"petal_width": 2.1
},
{
"key": "3",
"sepal_length": 5.1,
"sepal_width": 3.3,
"petal_length": 1.7,
"petal_width": 0.5
}
]
}
The Flow Designer’s Flow for this example would be like the following:
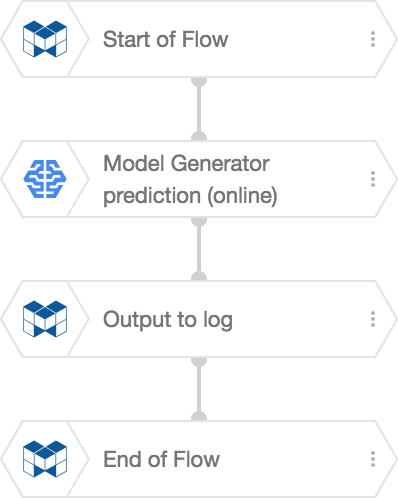
This simple Flow uses a Model Generator prediction (online) BLOCK to make predictions, then outputs the results using an Output to log BLOCK.
The following chart shows the properties for each BLOCK. It only includes properties that need to be changed from their default values.
| BLOCK | Property | Value |
|---|---|---|
| Start of Flow | ID | predict_iris |
| Model Generator prediction (online) | Model Generator | Select the Model Generator that will be used for the prediction |
| Input variable | _ |
|
| Output variable |
The variable that will store the results of the prediction. Since we are using |
|
| Output to log | Variable to output | _ |
The following is an example Unix curl command for executing the Flow:
curl -H 'Authorization: Bearer 951***a16' \
-H 'Content-Type: application/json' \
-d '{"_": [{"key": "1", "sepal_length": 5.9, "sepal_width": 3.0, "petal_length": 4.2, "petal_width": 1.5}, {"key": "2", "sepal_length": 6.9, "sepal_width": 3.1, "petal_length": 5.4, "petal_width": 2.1}, {"key": "3", "sepal_length": 5.1, "sepal_width": 3.3, "petal_length": 1.7, "petal_width": 0.5}]}' \
https://***.magellanic-clouds.net/flows/predict_iris.json
A response like the following will be returned if the Flow executes successfully. The 1 portion of the "job_id" will change each time the Flow is executed, so it doesn’t matter if there is a different value than shown here.
{"result":true,"job_id":1}
The following is a portion of the resulting Flow execution log:
`
{
"predictions": [
{
"score": [
0.017606934532523155,
0.9281915426254272,
0.05420156940817833
],
"key": "1",
"label": 1
},
{
"score": [
0.0002792126906570047,
0.2558387219905853,
0.7438820004463196
],
"key": "2",
"label": 2
},
{
"score": [
0.9730234146118164,
0.026976602151989937,
6.675784813836572e-09
],
"key": "3",
"label": 0
}
]
}
Providing input data when externally executing Flows (x-www-form-urlencoded)
This method sends input data as parameters when externally executing a Flow to make predictions.
External Flow execution refers to using a Web API to execute a Flow. The method for making predictions introduced here passes input data with the Content-Type header set to x-www-form-urlencoded in the HTTP request.
You can reference parameters that have been sent to a Flow by using variables with the same names as the parameters. We can prepare our data using these variables within the Construct object BLOCK.
For example, see the following Construct object BLOCK and its Data property:
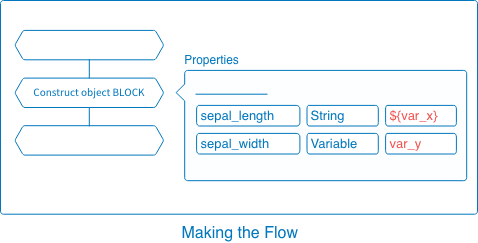
If we send the parameters var_x=5.9 and var_y=3.0 when we execute this Flow from an external source, the values will change as follows:
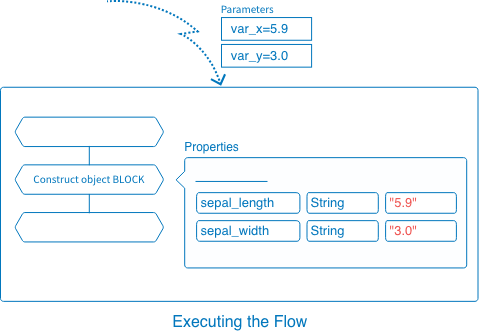
${var_x}becomes"5.9", the value of the parametervar_x.-
var_ybecomes"3.0", the value of the parametervar_y.
Variableis handled as aString.
info_outline Parameter values are all handled as strings.
By referencing variables with parameters, we can change the data created each time the Flow executes.
Setting the BLOCK's Data property to some types (numerical value, month, day) will cause it to expect numbers rather than strings. However, passing numbers that have been converted to strings, such as "5.9" or "0", will not cause any problems.
The Model Generator prediction (online) BLOCK converts strings into numerical values for items where it expects a numerical value. However, strings like "one" or "abc" that cannot be converted into a number will not work and will cause the prediction to fail.
We’ll create the following Flow in a Flow Designer for our Machine Learning prediction:
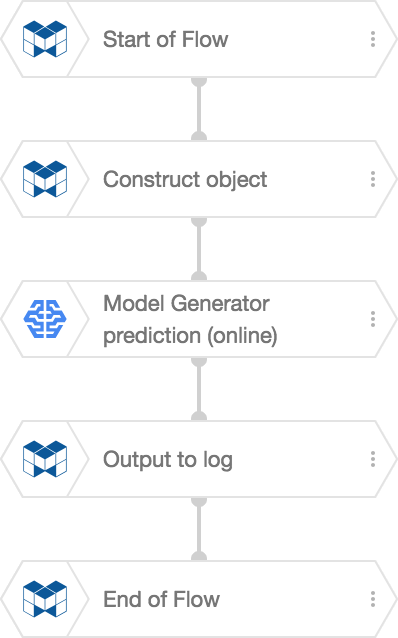
The Construct object BLOCK will use parameters sent to the Flow when it was externally executed to create the input data. The Model Generator prediction (online) BLOCK then uses this input data to make predictions. The Output to log BLOCK prints a log containing the prediction results.
The following chart shows each BLOCK’s property settings. It only contains properties that must be changed from their default values:
| BLOCK | Property | Value | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Start of Flow | ID | predict_iris | |||||||||||||||||
| Construct object | Results variable | _ |
|||||||||||||||||
| Data |
This example uses Variable expansion to set each the values as the parameters sent to the Flow. We've used the same names for the input data's items (key) and parameters in order to keep things simple. |
||||||||||||||||||
| Model Generator prediction (online) | Model Generator | Select the Model Generator that will be used to make predictions. | |||||||||||||||||
| Input variable | _ |
||||||||||||||||||
| Output variable |
info_outline We're using the same variable, |
||||||||||||||||||
| Output to Log | Variable to ouput | _ |
The following Unix type curl command executes a Flow and passes input data parameters (the -d "xxx=#" portion):
curl -H "Authorization: Bearer 951***a16" \ -d "key=1" \ -d "sepal_length=5.9" \ -d "sepal_width=3.0" \ -d "petal_length=4.2" \ -d "petal_width=1.5" \ https://***.magellanic-clouds.net/flows/predict_iris.json
A response similar to the one below will come after the Flow successfully executes. The 1 for the "job_id" portion changes each time the Flow executes, so it's not a problem if you try out the example on this page and receive a different number.
{"result":true,"job_id":1}
The following is a portion of the resulting log:
{
"predictions": [
{
"score": [
0.017455093562602997,
0.7145982980728149,
0.26794660091400146
],
"key": "1",
"label": 1
}
]
}

