精度の評価と評価指標について（分類編）

グルーヴノーツのコンサルタント吉村です。

前回の「精度の評価と評価指標について（回帰編）」の記事では、予測する結果が数値の場合の評価指標について書きました。下記の一つ目に当たります。

今回は、二つ目の予測する結果がカテゴリだった場合について説明したいと思います。

予測する結果がカテゴリということは

のシチュエーションになります。

予測する結果がカテゴリということは、数値回帰の時のように差（誤差）がありません。差が出ないということは「合っているか（True）／合っていないか（False）」をもとに、その個数（データ数）を使って考えていきます。

予測する結果が分類の場合（数値分類／画像分類）

今回は、100人の顧客にダイレクトメールを送付するのですが、なるべく購入してくれるお客さんにだけ送付したい。というビジネス上の目的で、「A：反応なし／B：来店した／C：購入した」を予測するシチュエーションで進めます。

まずは、正解（実績）と予測を比較する正誤表になります。（10件抜粋）

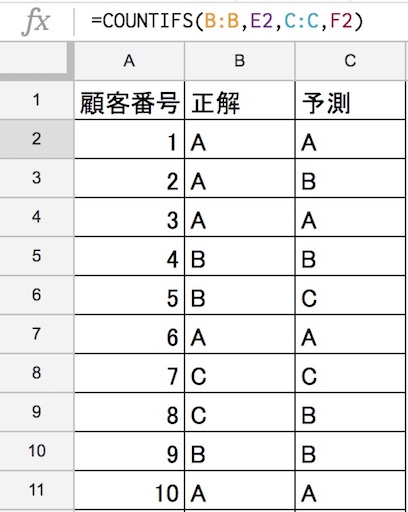
この表を見ると、1件ごとの結果について評価することが可能です。ただし全体としてどうなのかは、これでは分かりません。なので指標値にするのですが、その前に混同行列というものを作成します。

必須ではないのですが、理解の順番として混同行列を作る前に、正解と予測の集計表を作成します。

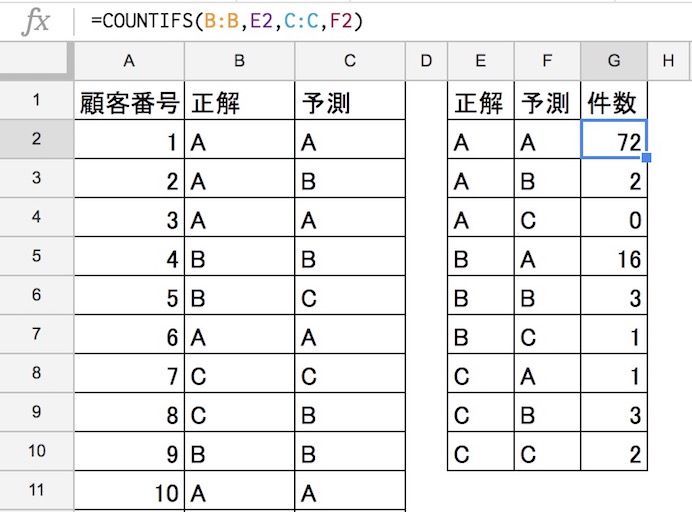
これをマトリクスに置き換えたものを、混同行列と言います。この混同行列の左上から右下へ、斜めの緑色のマスが正解で、残りの赤いマスが不正解です。

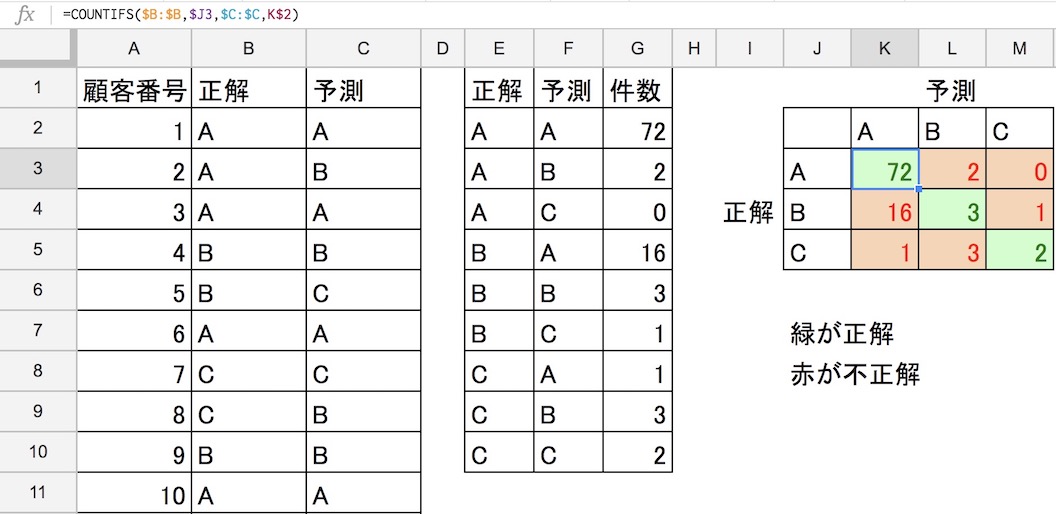
この混同行列を見ると、予測の得意なところと苦手なところがわかります。この例では正解がBなのに、Aと間違う部分が多いことがわかります。

集計列を追加してみました。こうすると、カテゴリごとの正解数と不正解数がわかります。この数を使って、指標値を計算していきます。

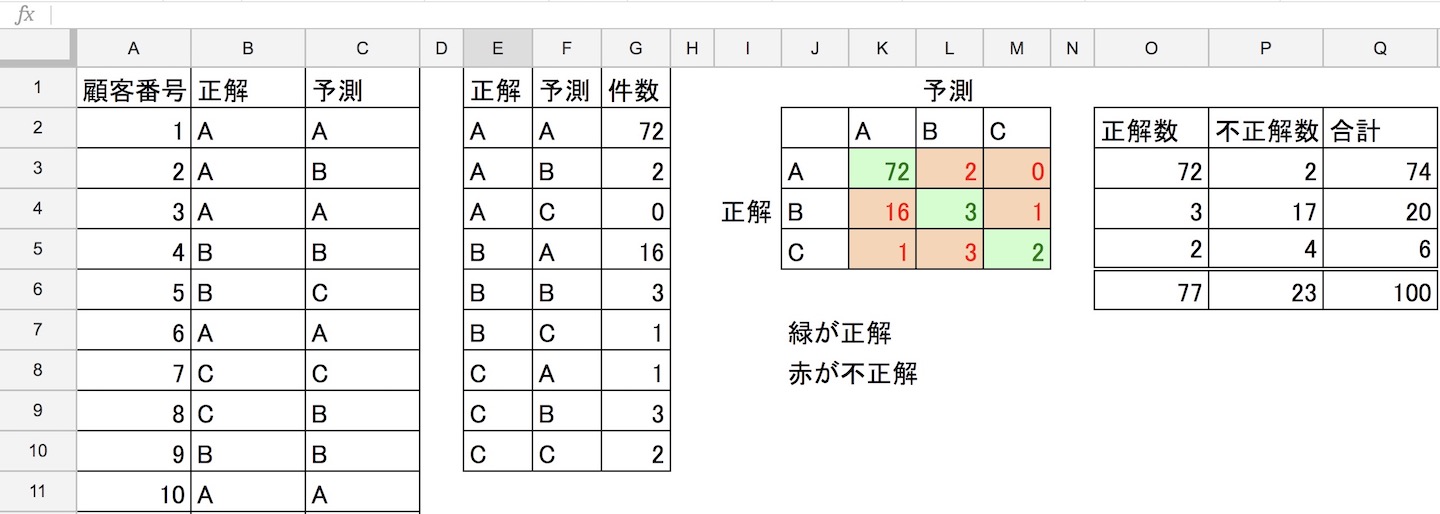
今回は、2つの評価指標を紹介します。

・全体精度（Overall Accuracy）

一般的に精度と呼ばれるもので、「正解数／データ数」で計算できます。※偏りのあるデータで適正に評価できないという問題があります。

・平均精度（Average Accuracy）

カテゴリごとの精度を平均値です。「Aの正解数／Aのデータ数」というように、カテゴリごとに精度を計算し足して、カテゴリ数で割ります。平均精度は、データ数の少ないカテゴリも評価へ反映できるという特徴があります。

どちらかを使うのであれば、平均精度は意図せず不適切な判断をせずにすむので、お勧めしています。

実際にそれぞれ計算してみましょう。

正解数／データ数なので全体の正解数 77 をデータ数 100 で割ります。
77 / 100 ＝ 0.77000
となります。

結果として精度77%というと、「なんとなくまぁまぁ」という感触になりますが本当にそうでしょうか？
実際には6人しか買ってくれるお客さんがいなくて、そのうち2人しか当てれていないのに77%といえるでしょうか？

このように、全体精度は偏りのあるシチュエーションでは適切な評価ができなくなります。
適切に評価をするために、平均精度を計算してみましょう。

まずカテゴリごとの精度の平均値を計算します。
Aの精度　→　72 / 74 ≒ 0.97297
Bの精度　→　 3 / 20 ≒ 0.15000
Cの精度　→　 2 / 6 ≒ 0.33333

次に、これらの平均値を計算します。
(72 / 74 + 3 /20 + 2 / 6) / 3 ≒ 0.48544

BやCの低い精度が反映できるので、適切に低い精度となりました。このように偏りがあるカテゴリを評価する場合には、平均精度を利用することをお勧めしています。

今回は機械学習にて分類予測を行った際に、評価する方法として取り扱いやすい2つの評価指標をご紹介しました。次ではないですが、応用編として実際にデータに偏りがある場合に機械学習で予測するためのデータの与え方や、予測モデルとしてのバランスの取り方を説明できたらいいなと思っています。

※本ブログの内容や紹介するサービス・機能は、掲載時点の情報です。