精度の評価と評価指標について（回帰編）｜グルーヴノーツ

グルーヴノーツコンサルタントの吉村です。

色々なお客様がMAGELLAN BLOCKSを用いて機械学習に取り組むお手伝いをしているなかで、時々言われることがあります。

当たり前ですが、皆さん精度について気になっているのかと思います。ただ、何%の精度が出たらOKというような閾値は存在しません。

「ビジネスに価値が出る」そこが判断基準です。

例えば販売数を予測する際に、平均誤差が20%発生している。しかし経験と勘に頼った今の運用では、ロスが25%出ている。この5%の差でロスが減り、コストが利益率を改善できるかもしれない。

また、ベテランの職人が機械の調整をするより少し間違いが多い。しかし「この人しかできない」を排除し、人員リスクを排除できるかもしれない。

など「勝手に期待する精度」より出ていなくても、ビジネスに価値が出る場合があります。取り組み方の記事で述べたとおり、「ビジネスの目的」を判断基準にすれば、自ずと適切な判断できます。

とは言うものの、精度を見て評価してあげる必要はもちろんあります。その際の評価方法について、ご説明いたします。

説明に入る前に、評価の考え方として大きく2種類の考え方があります。

今回は、まず1つ目の回帰の場合についてご説明します。

予測する結果が数値の場合（数値回帰）

予測する結果が数値（数値回帰）か、カテゴリ（数値分類／画像分類）かによって、評価方法が変わります。分類の方が難しくなるので、今回はまず、回帰編のご説明をします（分類編は別の記事にて）。

予測する結果が数値ということは、95個売れると予測したときに実際には92個で余ったり、99個で足りなかったり誤差が発生します。1週間分の予測をするシチュエーションで考えて見ましょう。

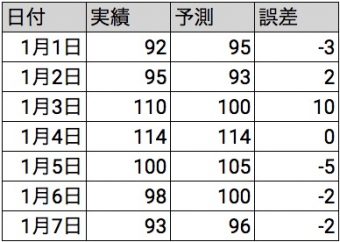
このように、7日間の実績と予測を比較すると毎日誤差が発生します。この誤差を平均化した値を、評価指標として考えます。平均なので合計してデータ数で割るわけですが、この誤差は合計するとゼロになってしまいます。もちろんこれで良いわけがありません。

このように、差し引きを発生させないための評価方法として、2つのよく使われる評価指標があります。

・平均絶対誤差（MAE：Mean Absolute Error）
　誤差の絶対値を平均したもの

・二乗平均平方根誤差（RMSE：Root Mean Squared Error）
　誤差の二乗を平均して平方根をとったもの

いずれもマイナスの値をプラスにすることを目的としていますが、統計などの世界ではRMSEの方が一般的に使われています。MAGELLAN BLOCKSのモデルジェネレーターで表示している誤差も、このRMSEになります。

それぞれの計算方法はこのようになっています。

まずは各データに対して誤差の絶対値を取ります。

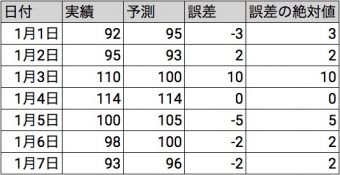
次に誤差の絶対値を合計します。
3 + 2 + 10 + 0 + 5 + 2 + 2 = 24

最後にデータの件数で割って平均を取ります。
24 / 7 = 3.428571428571429

これが絶対値平均誤差です。

まずは各データに対して誤差を二乗します。

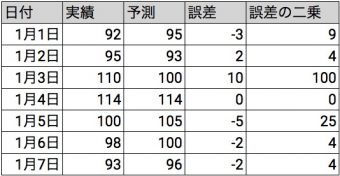
次に誤差の二乗を合計します。
9 + 4 + 100 + 0 + 25 + 4 + 4 = 146

続いてデータの件数で割って平均を取ります。
146 / 7 = 20.857142857142857

最後に平方根を取ります。
（20.857142857142857 の平方根）= 4.566962103755938

これが二乗平均平方根誤差です。二乗平均平方根誤差の方が大きくなりましたが、絶対値平均誤差に対して大きな誤差を厳しく評価する特徴があります。

ちなみに、二乗平均平方根誤差はExcelやGoogleスプレッドシートで簡単に計算できます。もとのこの表の状態で、Excel/Googleスプレッドシートどちらでもこの式で算出されます。

=SQRT(SUMPRODUCT(D:D,D:D)/(COUNTA(D:D)-1))

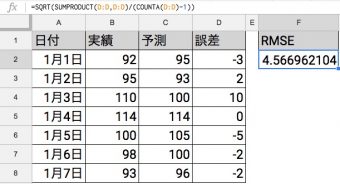
このように予測する結果が数値だった場合に利用する、2つの評価指標について説明しました。機械学習に取り組む際には、さらに誤差を小さくするために、予測因子を増やしたりデータを増やしたりします。例えば予測因子を増やして学習させて、再度予測した際に下表のような結果になりました。

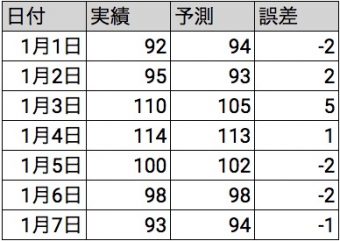
この結果に対して二乗平均平方根誤差をとると、2.47847879612821という結果が得られました。
前回の4.57→2.48へ、誤差が小さくなり精度が向上していることが判断できます。

こうやって試行錯誤のサイクルを繰り返す際には、どうしたら評価指標がどうなったか、を見ていくことが大事です。

予測する結果がカテゴリの場合（数値分類／画像分類）については、次の記事かその次くらいで説明したいと思います。

※本ブログの内容や紹介するサービス・機能は、掲載時点の情報です。